活性化関数をまとめた - 電電のブログ

はい電電です．

この前のブログで次回は褒めたもんにディープラーニングを適用する話を書くといったなあれは嘘だ．
（内容が多すぎてまとめきれてない）（早く書きます）

というかこのブログで機械学習とかに全く触れてこなかったのでいきなりNLP（自然言語処理）についてガリガリ書くよりジャブ的な意味もあります．

本音は活性化関数がこんがらがって来たからまとめたってだけです．

f:id:denden_seven:20190322025355p:plain — 活性化関数

これが活性化関数を同時に表示したものです。これはこんがらがりますわ。

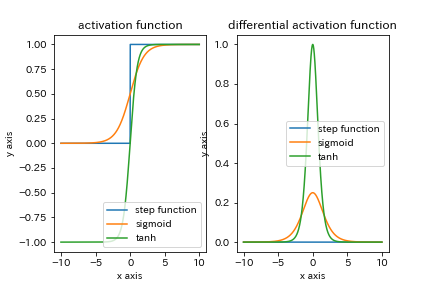
さて本題，活性化関数について話していきます．

活性化関数とはなんぞや？

具体的な活性化関数と利点，欠点

step 関数
sigmoid関数
tanh関数
Relu関数
leaky Relu関数
softmax関数

活性化関数とはなんぞや？

活性化関数とはニューラルネットワークを非線形の関数近似にしている部分であり，よく使われるシグモイド関数などはσ()とかき，これをニューラルネットに入力するベクトルをx，重み付けをW，バイアスをbとするとこのニューロンから求められる出力は，output = sigmoid(Wx+b)となります．
この時の重み付けWとバイアスｂの値を更新していくことによって，学習が行われます．この活性化関数は非線形であることが求めらます．
なぜなら，この活性化関数部分が線形関数だとその出力も線形関数になってしまい，線形関数以外をうまく表現できないからです．
このように活性化関数はパーセプトロンを用いた計算において非線形化という非常に重要な役割を持っています．
しかしながら似たような関数が多く，こんがらがるのでまとめます

具体的な活性化関数と利点，欠点

step関数

$y= \begin{cases} 0 (x<=0)\\ 1 (x>0) \end{cases}$

f:id:denden_seven:20190322005439p:plain — step関数

左の図は関数の形状，右図はxで微分した関数を示しています．

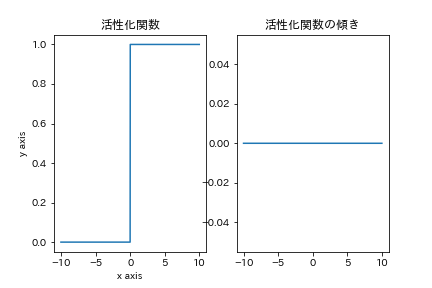
一番シンプルな非線形活性化関数です. 傾きが原点以外に存在せず学習が効率的に行えないために後述のシグモイド関数の方が使われます．

sigmoid関数

$y = \frac{1}{1+e^{-x}}$

f:id:denden_seven:20190322005442p:plain — sigmoid関数

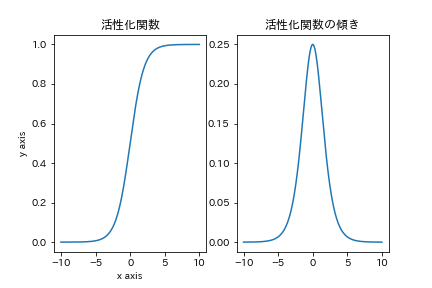
sigmoid関数です．
σ()でよく表せられたりします．この関数の出力は(0,1)におさまり，傾きがどのxについても存在しますが，関数が原点を通らないためにこの関数を通した，データの分布がいびつになります．
また，傾きの最大値が x=0 のとき 0.25 であるために，階層を深くしていくと勾配が単調減少するため勾配消失が起きるという問題があります．

tanh関数(双曲線関数)

$y = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}$

f:id:denden_seven:20190322011151p:plain — tanh関数

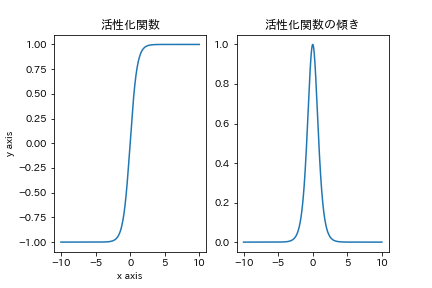
tanh関数はさきほどのsigmoid関数と形状がとても似ています．が大きく異なる点が二つあり，それらがよりよい性質となっています．一つ目は原点に関して点対称な関数であること．
二つ目は傾きの最大値が１であることです．これにより，勾配消失がsigmoidよりも起きにくく，より階層が深く作れます．

relu関数

$y= \begin{cases} 0 (x<=0)\\ x (x>0) \end{cases}$

f:id:denden_seven:20190322010451p:plain — relu関数

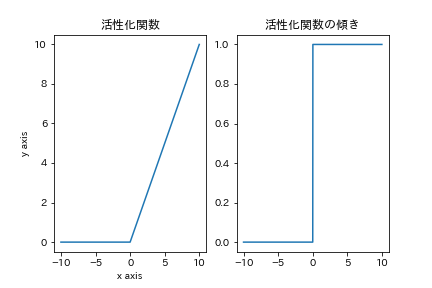
これは先ほどとは大きく異なった形状の関数となっています．しかしながらこのrelu関数は多くの場合で使われています．利点としては x>0 において傾きが１であるために先ほどのtanh関数よりも勾配消失が起きないこと．また傾きが１であることによる計算機の節約が狙えます．しかしながら x<0 においての情報を全て無くしてしまうためにこの部分の学習が遅いことが問題としてあります．

このreluの問題についてはdying reluとして存在している

参照dying ReLU について学ぶ - Qiita

leaky relu関数

$y= \begin{cases} -0.01x (x<=0)\\ x (x>0) \end{cases}$

f:id:denden_seven:20190322005417p:plain — leaky relu関数

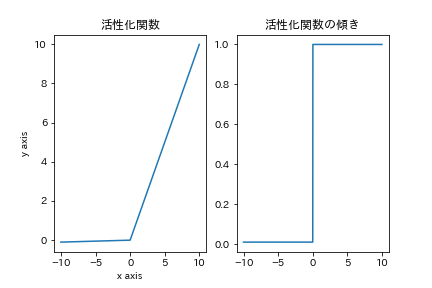
leaky relu関数は先ほどあげたrelu関数の弱点を補う形で生まれた. x<0 において勾配情報が消失してしまうことを防ぐために，その範囲において任意に傾きを指定する形．（今回は-0.01とした）

softmax関数

$y(x_i) = \frac{e^{x_i}}{\sum_{i=1}^{k}e^{x_i}}$

f:id:denden_seven:20190322022207p:plain — softmax関数

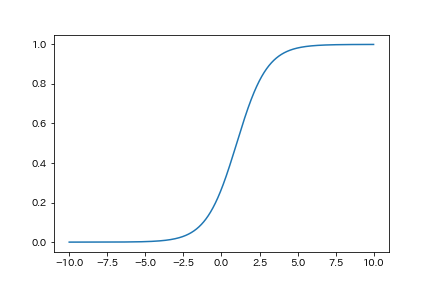
softmax関数です．これが一番他こんがらがるんですよね．まず上図で示しているsoftmax関数は間違いじゃないですけど，不完全です．なぜかっていうとこのグラフは入力している x_i が二つでありそのうちの一つを x_0 = 1 と固定してx_1 をｘとして考えた時のグラフです．実際は入力するx_iの値がそれぞれに変化します．
しかしながらなぜこれがよく使われるかというと，全ての x_i に関しての関数の合計つまり

$\sum_{i=1}^{n}softmax(x_i)=\sum_{i=1}^{n} \frac{e^{x_i}}{\sum_{k=1}^{n}e^{x_k}} = 1$
となり，最後の出力層に使うことによって分類問題に使えるからです．
例えば動物の分類を行う際に
ねこ：いぬ：うま：かば＝[1:3:0.1:0.01]
のような値が得られていたとするとこれはsoftmax関数を使うことにより
ねこ：いぬ：うま：かば=[0.1091, 0.8063, 0.0444, 0.0402]
のように合計が1であり，また大小関係が元の数値に基づいた値に変換することができます．このためsoftmax関数は分類問題の出力層に使われます．